Schrodinger's Cat
Amministratore di condominio
Chi di voi li ha fatti?
Come vi son sembrati?
Sapete le soluzioni?
Come vi son sembrati?
Sapete le soluzioni?
fattiChi di voi li ha fatti?
Come vi son sembrati?
Sapete le soluzioni?
infatti non sono riuscito a farlo u_u , gli altri due però sono giusti!Di questi che hai detto mi ricordo che nel triennio c'erano quello della benzina, capelli e cavalletta.
Io ho messo benzina + 0,84%, capelli 40% e cavalletta 50 cm! (anche se quest'ultimo non so come l'avrebbe potuto fare qualcuno del biennio, io ho usato il coseno e goniometria l'ho fatta in terzo)

questi mi son venutifatti
Ti dico quelli che ho messo io:
1) 91 giorni
2) 8 metri
3) non l'ho fatto (area della corona circolare intorno all'esagono)
4) qui ho messo il numero meno 10 :(
5) 2/5 messo 1/2 :(
capelli: 40% maschi e castani
numeri da invertire non l'ho fatto
benzina ho messo + 0,84%
cavalletta non fatto
quello delle diagonali dell'esagono veniva radice quadrata di tre, tutto diviso per tre
triangolo con proporzione---> angolo di 60°
mazzo di carte: 1/40
non me ne vengono in mente altri, se me li ricordi ti dico come li ho fatti
si: tralasciando le mie scarse capacità grafiche (figura fatta di corsa con paint) il rettangolo è 4 volte il triangolo, il rettangolo è formato dai 3 triangoli uguali a quello considerato + un altro rettangolo che ha il lato minore che è 1/2 di a (perchè l'area del rettangolo è doppia di quella del triangolo con le stesse dimensioni, quindi se il lato è metà di a il rettangolino è equivalente al triangolo) ponendo che a sia lungo 2 a+b sarebbe 5, quindi 2/5 (correggetemi se sbaglio)Questo dei 2/5 è quello del rettangolo con a e b? Perchè a me viene 2/3!
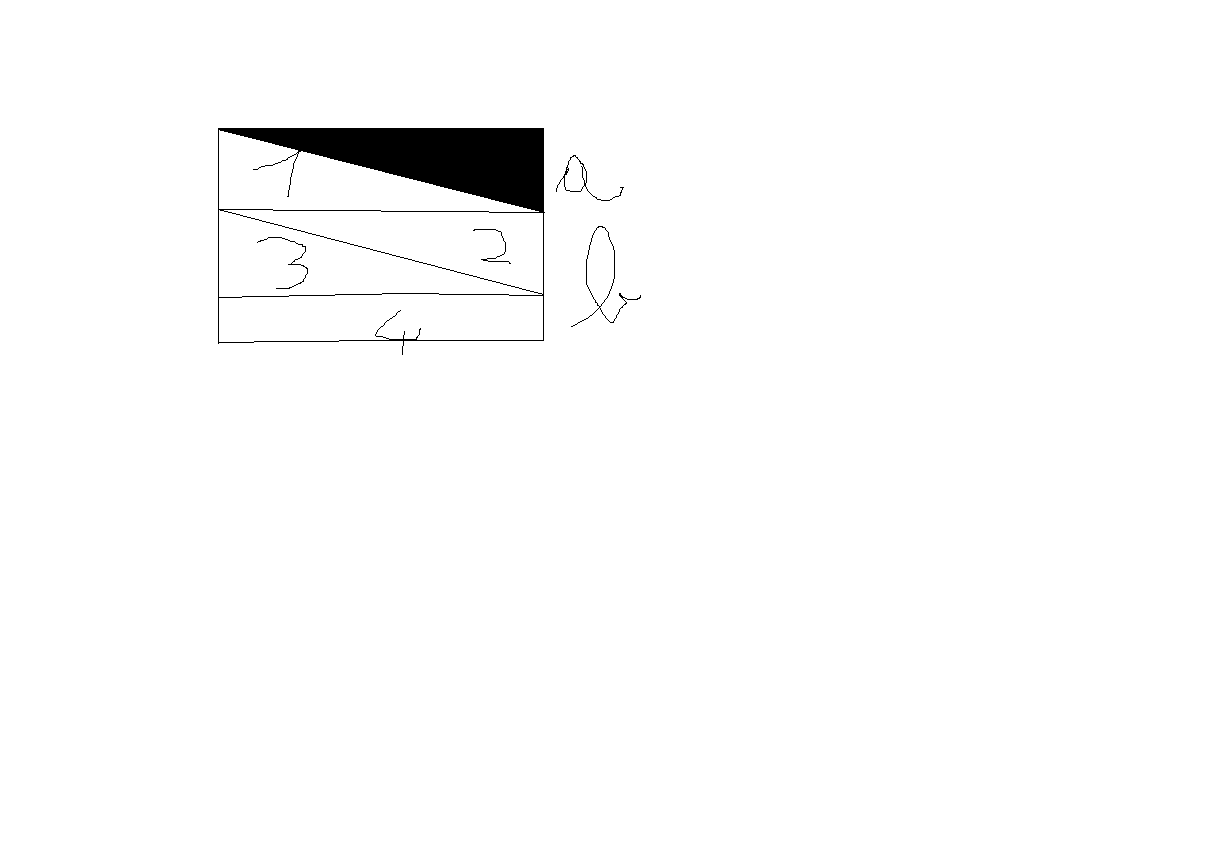
a me sembra giusto, forse ho sbagliato ioQuesto è stato il mio ragionamento!
ce ne sono di diversi: i giochi di archimede, i giochi d'autunno della Bocconi (2 giorni fa), i giochi di primavera e poi a volte qualcosa a livello regionaleI Giochi di Archimede sarebbero i giochi matematici che propongono sempre a scuola ogni anno?
L'ho fatto una volta in seconda media, ma quest'anno anche se mi sarebbe piaciuto non l'ho fatto perché pensavo sarei dovuto andare in una scuola di un paesino vicino come ho fatto alle medie e non avevo voglia di farlo perché tanto ero sicuro di non riuscire a passare tanto in là, ma poi oggi i due della mia classe che hanno partecipato sono andati nella mia scuola a farli e hanno pure saltato due ore di lezione D: Per questo vorrei partecipare l'anno prossimo à.à E anche perché mi piace abbastanza la matematica.
E quale di questi c'è stato oggi? Se può essere d'aiuto so che la finale è in Francia.ce ne sono di diversi: i giochi di archimede, i giochi d'autunno della Bocconi (2 giorni fa), i giochi di primavera e poi a volte qualcosa a livello regionale
io sono riuscito a farlo! Praticamente usciva che la figura percorsa dai salti era un triangolo equilatero di lato 40 cm più un prolungamento della base (il resto del salto) largo sempre 40 cm. Poi, andando verso l'alto, si arrivava ad avere 50 cm di distanza dal punto di partenza e da quello di arrivo.cavalletta 50 cm! (anche se quest'ultimo non so come l'avrebbe potuto fare qualcuno del biennio, io ho usato il coseno e goniometria l'ho fatta in terzo)
boh, io ho preso la squadra, mi sono fatto i passaggi e alla fine mi veniva lungo poco più di 60cm, ho calcolato che un po' di errori li avevo per forza fatti io e quindi ho messo 40 radice di 3oggi ho fatto i giochi del biennio. 14 su 16 (in due ore, rispetto ai 20 in 90 minuti degli anni scorsi... chissà perché) ^^
io sono riuscito a farlo! Praticamente usciva che la figura percorsa dai salti era un triangolo equilatero di lato 40 cm più un prolungamento della base (il resto del salto) largo sempre 40 cm. Poi, andando verso l'alto, si arrivava ad avere 50 cm di distanza dal punto di partenza e da quello di arrivo.
Quello dell'esagono è pi greco, mi sa. Un mio compagno ha seguito un ragionamento del tipo "radice di 3 al quadrato, quindi 4pi - 3pi = pi greco" e penso che abbia ragione.
Ho preso un punto e ho disegnato una piccola linea verso sinistra, il primo salto, e quindi dieci centimetri.ha ragione gamer, a/b=2/3. mi spieghi come hai fatto quello della cavalletta? io quelli così li leggo e li salto direttamente >.<
non sono sicuro, ma se li hai fatti giusti dovresti passareEDIT: io è il primo anno che faccio i giochi di archimede, 13/14 su 16 è un punteggio che permette mediamente di passare il turno?
erano 20 in due oreoggi ho fatto i giochi del biennio. 14 su 16 (in due ore, rispetto ai 20 in 90 minuti degli anni scorsi... chissà perché) ^^

viene 8 senza la radice:mi sono clamorosamente bloccato sul secondo (quello del triangolo isoscele con area 16 mquadrati) perchè...- boh, mi sono bloccato xD
alla fine ho messo 8 radice di 2, ma non mi convince...