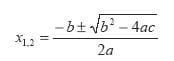secondo me è meglio una lezione lampo completa sulle equazioni di II grado.
la tipica equazione di II° si presenta nella forma:
ax^2+bx+c=0,
-a<>0 (altrimenti si ricondurrebbe a un'equazione di primo grado)
-se b=0 allora l'equazione di dice spuria, e ha risultati (chiamati radici) reali solo se c<0. infatti in caso contrario dovresti eguagliare un termine sempre positivo a uno negativo, cosa impossibile.
-se c=0 allora è possibile raccogliere una x e prende la forma x(ax+b)=0. quest'equazione avrà soluzioni x=0 e x=-b/a
se tutti e tre i termini sono diversi da zero è necessario trovare una nuova strada per risolvere il problema. risparmiandoci la dimostrazione otteniamo la formula per la risoluzione: x = [-b±radice(b^2-4ac)]/2a
b^2-4ac prende il nome di delta (Δ)
nel tuo caso: -2x² + 3x -1=0
Δ = 3^2 - 4(-1)(-2) = 9 - 8 = 1
la formula di risoluzione può essere quindi riscritta come x = [-b±radice(Δ)]/2a
se Δ>0 si avranno 2 soluzioni (chiamate radici) reali e distinte, se Δ=0 si avranno due soluzioni reali e coincidenti, se Δ<0 non si avranno soluzioni reali (l'equazione non è impossibile!!)
a cosa serve quindi il Δ nella geometria analitica?
il Δ serve a stabilire i rapporti fra una curva e una retta. mettendo a sistema l'equazione della curva con quella della retta si ottiene un'equazione di secondo grado. se il Δ di quest'equazione viene posto maggiore di 0 si otterranno 2 soluzioni che stabiliscono i punti di intersezione fra retta e curva. se Δ=0 si otterrà il punto di contatto della retta con la curva (due punti coincidenti). se Δ<0, non avendo l'equazione nessuna soluzione, la retta è esterna alla curva e non la interseca in nessun punto.
esaminiamo il caso della retta y=mx+q e della parabola y=ax^2+bx+c in un suo punto P(xo,yo)
mettendo a sistema l'equazione del fascio di rette passanti per P e mettendolo a sistema con la parabola si ottiene un'equazione in funzione di m. ponendo il Δ=0 otteniamo l'm della retta tangente, che inseriremo poi nell'equazione del fascio.
per facilitarci il compito, con lo studio delle derivate), l' m della retta y=mx+q tangente alla parabola y=ax^2+bx+c nel suo punto P(xo,yo) è: m=2axo+b
l'equazione della retta tangente in P sarà quindi: y = (2axo+b)(x-xo) + yo